The Official Inflection Point Calculator: Get an Answer Now

Are you looking for an inflection point calculator that works for any function? You’ve certainly come to the right place. I couldn’t find an inflection point calculator that worked on both simple and complex functions anywhere online, so I decided to build one myself. So give it a try below, it’s free to use.

Inflection Point Calculator

Enter a function of x:

The Background Behind Inflection Points

Inflection points represent key moments where things begin to change.

Although they may feel insignificant at times (like when you’re doing your homework), inflection points are certainly not just abstract math concepts. In fact, they are key to understanding the world around us.

Let me explain: whether you’re working with the curves of a bridge to the trajectory of a market trend, inflection points are everywhere. Noticing these points is crucial in fields like engineering, economics, and data analysis.

For example, in engineering, identifying inflection points helps in understanding material stress and strain. In addition, economists use them to interpret market dynamics, identifying turning points in financial graphs. And finally in education, they form a core concept in calculus, challenging students to think beyond mere formulas.

By the way, we have also have an awesome forecasting calculator if you ever need to predict the growth of something (like your business or website).

a math formula on a whiteboard with a hand writing it

What is an Inflection Point?

At its core, an inflection point is where a curve changes its bending direction.

Mathematically, it’s the point on a graph at which the curvature shifts from concave to convex, or vice versa. This change is detected through the function’s second derivative: an inflection point occurs where this derivative changes sign.

For example, to understand this better, consider the function f(x)=x³. Its graph bends downwards for negative values of x and upwards for positive values. Then, right at x=0, the graph changes its bending direction, making it an inflection point.

But why does this matter? Inflection points reveal more than just a change in direction; they provide insights into the function’s behavior. In the real world, these points can signify crucial changes — like a turning point in a business’s growth curve or the peak stress point in a physical structure.

Let’s take a practical example, such as a business’s revenue graph. An inflection point in this graph could indicate where the business shifted from a slow to rapid growth phase. This can be extremely useful for forecasting (we also have a calculator for this on this site). Identifying this point can certainly help analysts understand past performance and predict future growth patterns.

what is an inflection point thumbnail with the text an inflection point is a point on a curve where the curvature changes sign. for example, from concave to convex

The Challenge of Finding the Inflection Point

Finding inflection points can be tricky, especially for complex functions. The traditional method involves three steps: find the first derivative (the rate of change), then the second derivative (the rate of change of the rate of change), and finally, solve for points where the second derivative is zero or undefined, which signals the change in the curve’s concavity.

However, this process can be challenging, especially with complex functions. It also requires a deep understanding of calculus and can be time-consuming.

Manually solving the second derivative and analyzing its sign change is not always straightforward. For complex functions, the task becomes even more daunting, often necessitating computational tools for accuracy and efficiency.

For example, many functions, especially those encountered in higher-level mathematics or real-world applications, don’t easily give up their inflection points. They require more than just basic calculus; they often need computational tools to solve. This is where an Inflection Point Calculator becomes valuable. It simplifies this process, making it more accessible to students and professionals alike.

This is where the Inflection Point Calculator comes into play. It certainly simplifies this process, making it super easy for everyone — from experts to beginners. In the next sections, we will explore how the Inflection Point Calculator works, its benefits, and how to use it effectively with examples. We aim to provide a tool that makes finding inflection points less of a chore and more of a quick, reliable task.

a chalkboard of difficult math functions with inflection points — Say goodbye to the intense manual function calculations, and hello to quick and easy answers!

Introducing the Inflection Point Calculator

The journey to finding inflection points, while rich in learning, can be a tough climb, especially for those new to calculus or dealing with complex functions.

The inflection point calculator stands out for its straightforward approach to a typically complex process. We automated the calculations, so you can find inflection points seamlessly, freeing up your time from manual calculations.

answer to how do you find an inflection point with a calculator image and pencils with text saying to find an inflection point, consider where the second derivative changes signs.

Key Features of the Inflection Point Calculator: Accuracy, Ease of Use, and Versatility

Accuracy: At its core, the Inflection Point Calculator is built to deliver precise results. Whether it’s a simple polynomial or a more complex function, the tool meticulously computes the inflection points, ensuring high accuracy in its outputs.
Ease of Use: The calculator is designed with a user-friendly interface. Users can simply input their function, and the tool does the rest, eliminating the need for complex calculations and making the process accessible to everyone, regardless of their mathematical background.
Versatility in Handling Functions: One of the standout features of the Inflection Point Calculator is its ability to handle a variety of functions. From basic curves to more advanced equations, the tool is equipped to analyze different types of functions, making it a versatile asset for both educational and professional use.

How the Inflection Point Calculator Works

The Calculator operates on a straightforward principle. It first takes the user’s input function and computes its first and second derivatives. The crucial part of the process is identifying where the second derivative changes sign – a clear indicator of an inflection point.

To make this process more transparent, let’s break down a simple example:

Input Function: Consider the function: f(x)=x³−6x²+11x−6.
First Derivative: The calculator computes f′(x).
Second Derivative: It then calculates f′′(x) and analyzes it to identify where it changes sign.

The algorithm powering the calculator is designed to efficiently handle these steps, presenting you with clear, concise results. Additionally, a graph is plotted to visually demonstrate the function and its inflection points, further aiding understanding.

Step-by-Step Examples of Functions with Inflection Points

Illustrating the Calculator in Action

To showcase the effectiveness of the Inflection Point Calculator, let’s walk through the following examples:

Simple Function: 6f(x)=x³−6x²+11x−6
- Upon entering this function into the calculator, it outputs the inflection points and provides a graph for visualization. The graph clearly shows where the curve changes concavity, thus pinpointing the inflection points.
More Complex Function: f(x)=x⁴−10x³+35x²−50x+24
- For this function, the calculator again performs the calculations and presents the inflection points. The graph aids in understanding how the function behaves around these points.

These examples demonstrate the calculator’s ability to simplify what would otherwise be a time-consuming task, making the concept of inflection points more tangible and understandable.

Even More Examples of Different Inflection Points

Let’s jump into an example so you can learn how to handle these inflection point types of questions.

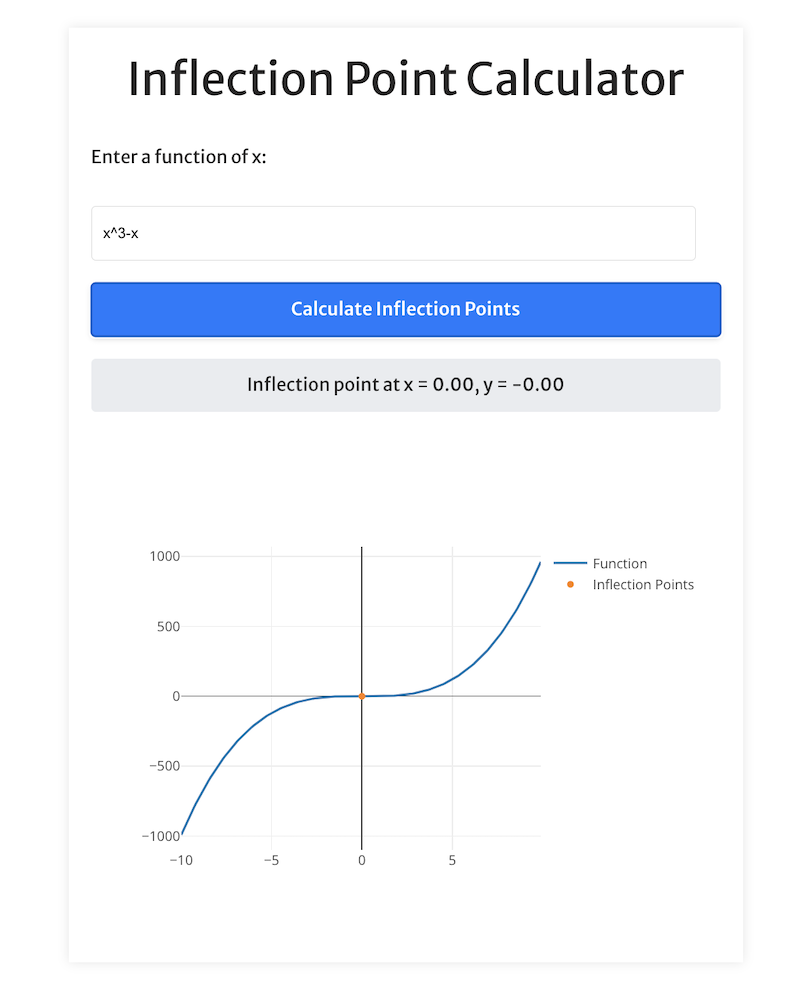
For example, let’s take the function f(x) = x³ – x.

To find the inflection points of a function, we first find its second derivative and then determine the points where this second derivative is zero (as these are the points where the concavity of the function changes).

The first derivative f'(x) is derived as follows: f'(x) = 3x² – 1
The second derivative f”(x) is: f”(x) = 6x

To find potential inflection points, we set the second derivative equal to zero and solve for x: 6x = 0

Solving this gives x = 0.

To confirm that x = 0 is indeed an inflection point, we check the sign of the second derivative on either side of this point. If the sign changes, it is an inflection point.

For x < 0 (for example, x = -1), f”(x) = 6(-1) = -6 (concave down).
For x > 0 (for example, x = 1), f”(x) = 6(1) = 6 (concave up).

Since the sign of the second derivative changes from negative to positive as we move from left to right through x = 0, this confirms that x = 0 is indeed an inflection point.

Finally, to find the corresponding y value, we substitute x = 0 back into the original function: f(0) = (0)^3 – (0) = 0

Therefore, the inflection point at x = 0.00, y = 0.00 is indeed correct for the function x³ – x.

How to Use the Inflection Point Calculator

Navigating the Tool with Ease

Using the Inflection Point Calculator is straightforward, making it an excellent resource for anyone needing to find inflection points quickly and accurately. Here’s a step-by-step guide on how to use it:

Accessing the Calculator: The tool is available online and can be easily accessed from any device with internet connectivity.
Inputting the Function: Enter your function into the provided input field. The calculator can handle a wide range of functions, from simple polynomials to more complex equations.
Initiating the Calculation: After entering the function, click the “Calculate Inflection Points” button. The calculator will process the input and compute the results.
Reading and Interpreting the Output: The results will display the inflection points, if any, of the given function. Alongside the numerical output, a graph will illustrate the function and highlight the inflection points for better visual understanding.
Tips for Best Results: For the most accurate results, ensure that the function is entered correctly. Double-check for any typographical errors in the equation before submitting.

This intuitive process makes the calculator an ideal tool for educational purposes, enabling students to explore and understand the concept of inflection points interactively.

screenshot of the inflection point calculator with a graph showing the inflection points of the function x^3-x — Example of the x^3-x function

The Biggest Advantages of the Inflection Point Calculator

Speed, Efficiency, and User-Friendliness

The Inflection Point Calculator offers several advantages over traditional methods of finding inflection points:

Speed and Efficiency: What used to take minutes or even hours now takes just seconds. The calculator quickly processes the input function and provides the results, saving valuable time and effort.
Handling Complex Functions: The tool is adept at handling functions that are too complex for manual calculation, broadening the scope of problems that can be tackled.
User-Friendly Interface: Its easy-to-use interface makes the calculator suitable for everyone, from students just starting with calculus to professionals who need quick results.

In the next sections, we’ll guide you on how to use the Inflection Point Calculator, followed by a call to action inviting you to try the tool and experience its benefits firsthand. Stay tuned as we dive deeper into making calculus not just easier, but also more approachable and engaging.

Discover the Power of the Calculator

Now that you’re familiar with the workings of the Inflection Point Calculator, it’s time to put it to the test. We invite you to try out the calculator with different functions. Experiment with both simple and complex equations to see how effectively and swiftly it identifies the inflection points.

Your feedback is invaluable. After using the calculator, we encourage you to share your experience. Let us know how it enhanced your understanding or simplified your work. Your insights will help us improve and continue providing tools that make complex mathematical concepts more accessible.

Don’t forget to share the Inflection Point Calculator with your peers, colleagues, or classmates. It’s a tool that can benefit a wide range of users, from students grappling with calculus concepts to professionals needing quick analytical insights.

Conclusion: Embracing Simplicity in Calculus

The Inflection Point Calculator is your ticket to getting the right inflection point answer faster.

Whether you’re a student, teacher, engineer, or just someone curious about calculus, the Inflection Point Calculator is designed to assist you in your mathematical journey. It’s a testament to how technology can transform our approach to learning and problem-solving, making even the most daunting mathematical tasks manageable and enjoyable.

As we continue to explore and innovate, tools like the Inflection Point Calculator will play a crucial role in making education more interactive, engaging, and effective. We hope this tool inspires you to delve deeper into the world of mathematics and discover its wonders with newfound clarity and ease.

Additional Resources on Inflection Points

For those interested in further exploring calculus and inflection points, here are some additional resources:

These resources provide comprehensive lessons and exercises to deepen your understanding of calculus and its various applications. Happy exploring!

More Free Calculators and Tools You Might Love

Useful Calculators

Baseball Calculators

Time from Today Calculator